버블정렬

개념

앞뒤로 이웃한 원소끼리 대소를 비교하여 위치를 교환하는 정렬방법이다.

인접한 두 원소를 비교하고 교환하는 작업을 PASS(패스)라고 한다. step, cycle이라고 부르는 사람들도 있던데.

알고리즘 (파이썬)

a = [6,4,3,7,1,9,8]  #정렬되지 않은 입력값

n=len(a)    #배열의 길이 

for i in range(0,n-1):  #pass
    for j in range(n-1,i,-1):
        if a[j] < a[j-1]:
            a[j], a[j-1] = a[j-1],a[j]  #교환

print(a)
>>>[1,3,4,6,7,8,9]

오름차순으로 정렬하는 버블정렬 알고리즘. 배열 맨 뒤부터 앞으로 탐색하며 비교, 필요 시 교환한다.

예시

입력 : 6 4 3 7 1 9 8

+는 비교 후 교환, -는 비교하나 교환은 안함.

PASS1.
6 4 3 7 1 9 +8
6 4 3 7 1 -8 9
6 4 3 7 +1 8 9
6 4 3 +1 7 8 9
6 4 +1 3 7 8 9
6 +1 4 3 7 8 9
1 6 4 3 7 8 9

PASS2.
1 6 4 3 7 8 -9
1 6 4 3 7 -8 9
1 6 4 3 -7 8 9
1 6 4 +3 7 8 9
1 6 +3 4 7 8 9
1 3 6 4 7 8 9

PASS3.
1 3 6 4 7 8 -9
1 3 6 4 7 -8 9
1 3 6 4 -7 8 9
1 3 6 +4 7 8 9
1 3 4 6 7 8 9

PASS4.
1 3 4 6 7 8 -9
1 3 4 6 7 -8 9
1 3 4 6 -7 8 9

PASS5.
1 3 4 6 7 8 -9
1 3 4 6 7 -8 9

PASS6.
1 3 4 6 7 8 -9

버블정렬 결과 :
1 3 4 6 7 8 9

버블정렬 비교 횟수 :
(n-1) + (n-2) + (n-3) + … + 1 = n(n-1)/2

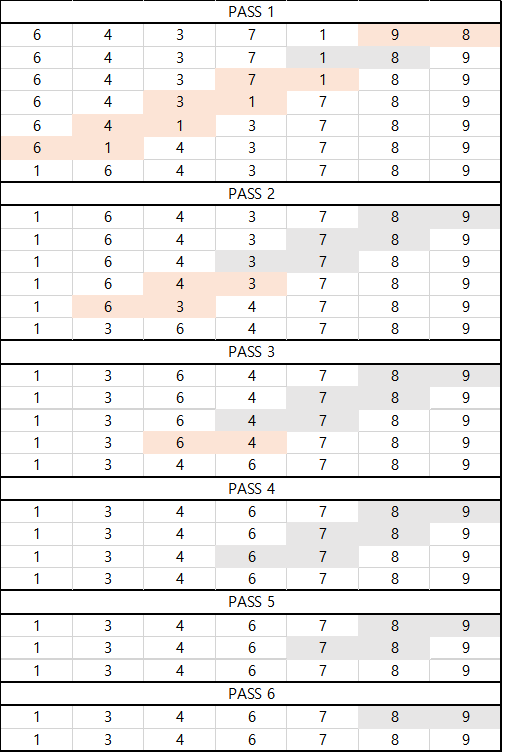
이미지로 정리한 결과. 빨간 색은 교환이 일어난 것을 표시하고, 회색은 비교하나 교환은 이루어지지 않음을 표시한다.

시간 복잡도

버블정렬의 시간복잡도는 O(n^2)이다.

알고리즘 개선 1. 조기 종료 조건

예시에서 PASS3 종료 후 모든 원소가 정렬되었음을 알 수 있다.

그러나 처음의 알고리즘은 원소가 이미 모두 정렬된 것을 인지하지 못하고 불필요한 비교를 계속 시행한다(PASS4~6)

개선: PASS 수행 시 비교 카운트를 체크한다. 비교 카운트는 원소 교환 시 1씩 증가한다. (또는 플래그; 0또는 1)

만약 비교 카운트가 0이면 모든 원소가 정렬되었다고 판단하고 정렬을 종료한다.

a = [6,4,3,7,1,9,8]  #정렬되지 않은 입력값

n=len(a)    #배열의 길이

for i in range(0,n-1):  #pass
    chk=0   #pass에서 교환한 횟수 (또는 플래그)
    for j in range(n-1,i,-1):
        if a[j] < a[j-1]:
            a[j], a[j-1] = a[j-1],a[j]  #교환
            chk+=1  #또는 chk=1
    if chk==0:  #교환 횟수가 0이면 탈출한다.
        break

print(a)
>>>[1,3,4,6,7,8,9]

각 pass에서 원소의 위치 교환이 이루어졌는지 체크하기 위해 chk 변수를 사용했다.

바깥쪽 for문 다음에 배치하여 각 pass가 시작할 때마다 0으로 초기화된다.

위에서 사용했던 값과 같은 입력 6,4,3,7,1,9,8을 입력하면, PASS4까지 수행하고 알고리즘을 종료한다.

비교만 하고 교환은 이루어지지 않으니 chk값이 증가하지 않을 것이고,

break문에 걸려서 반복을 탈출 할 것이다.

알고리즘 개선 2. 검사 범위 건너뛰기

입력이 1,3,6,4,8,9,7이라고 생각한다.

PASS1.

1 4 3 8 6 7 -9
1 4 3 8 6 -7 9
1 4 3 8 +6 7 9
1 4 3 -6 8 7 9
1 4 +3 6 8 7 9
1 -3 4 6 8 7 9

PASS1 종료 후 결과: 1 3 4 6 8 7 9

1, 3, 4, 6은 이미 정렬되어 다시 확인할 필요가 없다. 하지만 기존 알고리즘으로는 맨 앞 원소(1)를 제외한 나머지 부분을 다시 검사할 것이다.

개선 : 마지막으로 교환이 이루어진 인덱스를 저장한 후, 해당 인덱스까지만 비교하고 교환하도록 범위를 줄인다.

a = [6,4,3,7,1,9,8]  #정렬되지 않은 입력값

n=len(a)    #배열의 길이
k=0

while k < n-1:
    last=n-1    #각 pass에서 마지막으로 원소 교환이 이루어진 위치
    for j in range(n-1, k, -1):
        if a[j-1] > a[j]:
            a[j-1], a[j] = a[j], a[j-1] #인접한 두 원소의 위치 교환
            last = j    #마지막으로 원소 교환이 이루어진 인덱스를 저장한다
    k = last

버블정렬 변형 : 셰이커 정렬 (shaker sort)

양방향 버블정렬, 칵테일 정렬, 칵테일 셰이커 정렬 등등.. 부르는 이름이 많다.

셰이커 정렬은 매 pass마다 탐색방향을 바꾼다.

예시.
짝수 pass일 때는 배열의 앞->뒤로 이동하며 가장 큰 값을 가지는 원소를 뒤쪽으로 배치

홀수 pass일 때는 배열의 뒤->앞으로 이동하며 가장 작은 값을 가지는 원소를 앞으로 배치

a = [6,4,3,7,1,9,8]

left = 0  #배열의 처음 인덱스
right = len(a)-1  #배열 마지막 인덱스
last=right  #마지막으로 교환이 이루어진 위치

while left < right:
    for j in range(right, left,-1): #뒤에서 앞으로, 작은 수를 가진 원소를 앞으로 이동
        if a[j-1] > a[j]:
            a[j-1], a[j] = a[j], a[j-1]
            last=j
    left=last

    for j in range(left, right):
        if a[j] > a[j+1]:   
            a[j], a[j+1] = a[j+1], a[j] #큰 값을 뒤로 이동
            last=j
        right=last

칵테일 정렬의 시간복잡도 또한 O(n^2)이다.