5장. 훈련 노하우를 배웁니다
Do it! 정직하게 코딩하며 배우는 딥러닝 입문을 읽고 정리
이번 챕터는 모델의 정확도를 높이기 위한 여러가지 방법들을 소개한다.
모델 튜닝
데이터셋에 대한 적절한 모델을 선택했다면, 모델의 정확도를 높이기 위해 세부적인 사항들을 조절해야 한다.
(ex. 학습률, 손실함수의 종류 등등…)
이러한 값들을 하이퍼 파라미터라 한다.
테스트 세트로 모델 튜닝 시 문제점
이전 챕터까지는 전체 데이터셋을 훈련 세트와 테스트 세트로 나눴다.
테스트 세트를 사용하여 모델의 성능을 조정하는 경우, 모델이 테스트 세트에만 좋은 성능을 낼 수 있다.
이러한 경우 모델의 일반화 성능(generalization performance) 이 떨어졌다고 말한다.
모델 튜닝을 위해 테스트 세트가 아닌 다른 데이터 세트를 사용하여 해결할 수 있다.
검증 세트 (validation set)
검증 세트는 테스트 세트를 사용하기 전 모델을 튜닝하는 용도로 사용하는 데이터 세트이다.
훈련세트의 일부를 분리하여 검증세트를 만들어낸다.
주의해야 할 것은, 훈련세트의 크기가 너무 작아지지 않는 것이다.
사이킷런의 train_test_split() 함수를 사용하여 데이터셋을 쉽게 분리할 수 있다.
전체 데이터셋이 주어졌을 때,
- 훈련세트 - 테스트세트로 분리(8대2 비율)
- 훈련세트를 훈련세트/검증세트로 분리 (8대2 비율)
from sklearn.model_selection import train_test_split
과대적합과 과소적합
과대적합 (overfitting)
모델이 훈련 세트에는 높은 성능을 내지만,
검증 세트에는 낮은 성능을 내는 경우를 뜻한다.
과소적합 (underfitting)
훈련세트와 검증세트의 성능 차이가 크게 나지는 않지만,
전체적인 성능이 낮은 경우를 말한다.
가중치 규제 (regularization)
가중치 규제는 모델의 가중치가 너무 커지지 않도록 하는 방법이다.
L1 규제
손실함수에 가중치의 절댓값인 L1 norm을 더한다.
L1 규제는 Lasso(라소) 규제라고도 부른다.
L1 norm \({\parallel{w}\parallel}_1 = \sum_{i=1}^n {\left| w_i \right|}\)
로지스틱 손실함수 $L$에 L1 norm을 더하면,
\[L = -(ylog(a)+(1-y)log(1-a)) + \alpha {\sum_{i=1}^n \left|{w_i}\right|}\]여기서 $\alpha$는 L1 규제의 양을 조절하는 하이퍼 파라미터이다.
L1 규제를 파이썬 코드로 표현하면,
w_grad += alpha * np.sign(w)
#np.sign()은 요소의 부호를 반환한다.
L1 규제는 가중치를 0으로 만들 가능성이 있어, 많이 사용되지 않는다.
L2 규제
손실함수에 가중지의 절댓값 제곱을 더한다.
L2 규제는 Lidge(릿지)규제라고도 부른다.
L2 norm \({\parallel{w}\parallel}_2 = \sqrt{\sum_{i=1}^{n} {\left|{w_i}\right|}^2}\)
로지스틱 손실함수에 L2 norm을 더하면,
\[L = -(ylog(a)+(1-y)log(1-a)) + {1 \over 2}\alpha {\sum_{i=1}^{n} {\left|{w_i}\right|}^2}\]$\alpha$는 규제의 양을 조절하기 위한 하이퍼 파라미터이고,
계산을 편하게 하기 위해 루트를 없애고 $1\over2$를 추가했다.
L2 규제를 파이썬 코드로 표현하면,
w_grad += alpha * w
#L2는 가중치 값 자체를 사용한다.
교차검증 (cross validation)
전체 데이터셋의 크기가 너무 작아서,
훈련 세트가 너무 부족해질 때 사용하는 모델 학습 방법이다.
k-fold 교차검증
교차검증 중 책에서 소개된 방법인 k-폴드 교차검증은,
전체 데이터셋을 k개의 부분집합으로 나눈 후 부분집합이 한번씩 검증 세트로 사용될 수 있도록 하는 것이다.
이 때 나누어진 부분집합을 폴드라고 한다.
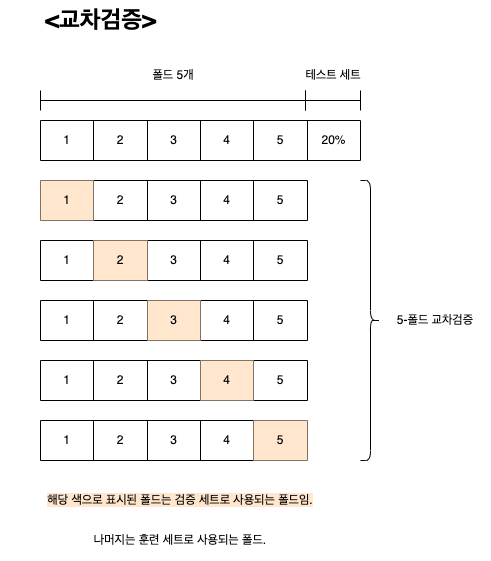
k-폴드 교차검증
- 전체 데이터셋을 k개의 부분집합으로 나눈다.
- 1번 부분집합을 검증 세트로 활용하고 나머지 (k-1)개를 학습에 사용한다.
- 모델 훈련 후 검증세트로 평가한다.
- 순서대로 부분집합 하나를 검증세트로 활용하여 반복한다.
- 모든 부분집합이 한번씩 검증세트로 활용된 후 최종적으로 평균을 낸다.
