4장. 분류하는 뉴런을 만듭니다 - 이진 분류
Do it! 정직하게 코딩하며 배우는 딥러닝 입문을 읽고 정리
이진분류 (binary classification)
임의의 샘플 데이터를 True 또는 False(0 또는 1)로 구분하는 문제를 말한다.
ex) 과일 데이터가 주어졌을 때, 그 과일이 사과인지(True) 아닌지 (False) 판단하는 것.
여러 클래스를 분류하는 다중분류는 7장에서.
퍼셉트론
- 이진 분류 문제를 해결하기 위한 초창기 알고리즘
- 선형 회귀와 유사한 구조를 가지지만, 마지막 단계에서 출력값을 계단 함수에 통과시키는 것이 차이잠
- 계단함수를 통과한 값은 가중치와 절편 업데이트에 사용
계단 함수
- 그래프 표현
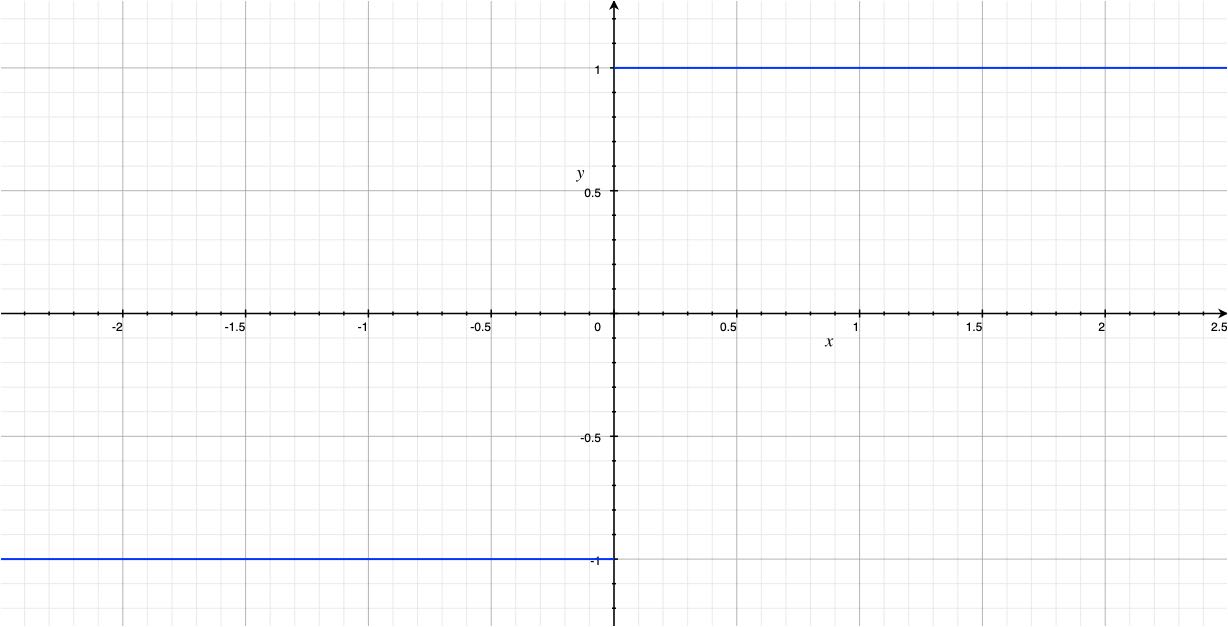
- 수식 표현
계단함수는 출력이 0보다 크거나 같으면 1, 작으면 -1을 내보낸다.
다른 책에서는 -1 대신 0으로 표현하는 경우도 있다. (1 or 0) .
퍼셉트론 연산의 표현
- 입력하는 특성이 n개일 때, 퍼셉트론 연산을 표현하는 수식:
- (b: 편향, w: 가중치, n: 특성의 개수, z: 선형함수 계산의 합)
아달린(Adaline)
- 퍼셉트론을 개선한 분류 알고리즘
- 역방향 계산을 선형함수 통과 이후 실행
로지스틱 회귀 (logistic regression)
- 명칭은 회귀지만 사실은 분류하는 알고리즘임
- 선형계산의 출력을 활성화 함수에 통과시켜 0과 1사이의 확률로 변환 -> $z$
- 활성화함수의 출력값을 임계함수에 통과시켜 0또는 1의 이진값으로 변환 -> $\hat{y}$
로지스틱 손실 함수
$L = -(ylog(a)+(1-y)log(1-a)$
(y:타깃, a:활성화함수 출력값)
$L=\begin{cases} -log(a), & y=1 \ -log(1-a), & y=0\end{cases}$
-
목표 : 로지스틱 손실함수 L의 값을 최소화 하는 것. L의 값을 최소화하는 w와 b를 찾는 것
${dL \over dw_i} = -(y-a)x_i$
${dL \over db} = -(y-a) \cdot 1$
- 제곱오차의 결과와 비슷함
- 제곱오차의 $\hat{y}$이 $a$로 바뀐 것이 차이점
- 정확도 (accuracy)
전체 테스트 셋 중에서 올바르게 예측한 샘플의 비율
